Szörnyetegalakzatok
A fraktálokkal való megismerkedésem fő motivációja kezdetekben természetesen az volt, hogy ezek a színes, monumentális, első ránézésre is végtelenül komplex, érdekes alakzatok vizualitása lenyűgözött, ám a velük való akárcsak laikus színtű foglalkozás is már figyelemreméltó matematikai felkészültséget igényel. Szóval hamar rájöttem, hogy mélyebben bele kell ásnom magam a témában.
Részben ez a komplexitás az oka annak is, hogy a fraktál-képekből nem lett „művészet“, és már csak a komputer-technikától való erős függésük miatt is e képek többnyire megmaradtak bizonyos matematikai számítások elektronikus „kijelzéseinek“. Azonban ha túllépünk az alakzatok esztétikai, dekoratív jellegén véleményem szerint érdekes lehet a fraktál-képek művészeti értékén elgondolkozni.
Mi is a fraktál?
A fraktálok „önhasonló”, végtelenül komplex matematikai alakzatok, melyek változatos formáiban legalább egy felismerhető, tehát matematikai eszközökkel leírható ismétlődés tapasztalható. A mai napig nincs egységes megállapodás a fraktálok pontos matematikai definíciójáról, illetve a fraktál fogalma nem csak a matematikai algoritmusok alapján pontosan kiszámított alakzatokat foglalja magába, hanem a nem teljesen szigorú önhasonlóságra épülő szerkezeteket is. Erre a természetben számtalan példát találunk, mint mondjuk a hópihék, vagy a páfrány levelek.
Egy speciális rekurzív művelettel, iterálással kapjuk őket, ami egy függvény ismételt végrehajtását jelenti az előző függvényértéken. Így az eredmény egy adott absztrakt objektum lesz, ami önhasonló módon sokszorozódik. Önhasonlónak, vagy fraktál tulajdonságúnak akkor nevezünk egy alakzatot, ha a mérési pontosságot finomítva (azaz az iterálást egyre tovább folytatva) ugyanolyan szerkezettel találkozunk, mint a finomítás előtt.
Korai fraktálalakzatok
A 19. században a fraktálok még egy igencsak utálatos területét képezték a matematikának, inkább kellemetlenségnek és vitaalapnak számítottak. Szörnyetegalakzatoknak is nevezték őket, mivel a függvénytan akkori eszköztára számára kivételes, az intuíciónak ellentmondó eseteket, problémát és kihívást jelentettek. Majd a századfordulóhoz közeledve készültek leírások részletesebben vizsgált alakzatokról.
A 20. század első felében az angol származású Lewis F. Richardsonnak a világ térképein az országhatárok hosszának pontosságát vizsgálva feltűnt, hogy néhány ország leírásában eltérnek egyes partvonalak hosszai. Ennek magyarázata az, hogy eljárástól és mérőeszköztől függően más és más eredmények kaphatók. Minél kisebb szakaszokat illesztünk a határvonalakra, azok annál hosszabbak lesznek, és ennek a növekedésnek nem lesz határa. Így, ha az (elméleti) mérésnél a felbontás végtelen kicsi lenne, akkor a becsült hossz végtelen naggyá válna.


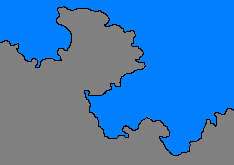
De miért is olyan furcsa ez? Azért, mert az eddigi matematikai modelleket, hagyományos geometriai alakzatokat vizsgálva ez a jelenség nem volt megfigyelhető. Például egy körívet egyre közelebbről szemlélve azt tapasztalnánk, hogy egyre hasonlatosabb lesz egy egyenes szakaszhoz, végtelen felbontáshoz tartva pedig egyenes vonal lesz belőle. A természet struktúrája viszont azt mutatja, hogy ha közelről nézünk valamit, ahelyett, hogy kisimulna, még érdesebb, részletgazdagabb lesz.
A partvonal probléma egy lehetséges matematikai modellje a Koch-görbe:

Képzeljünk el egy háromszöget, amelynek mindegyik oldala 1 m hosszú. Képzeljünk most el egy átalakítást is - egy sajátos, jól meghatározott, könnyen ismételhető szabálysorozatot: vegyük minden oldalnak a középső harmadát és emeljünk rá egy ugyanilyen oldalhosszú (azaz az eredetihez képest harmad akkora) egyenlő oldalú háromszöget. Az eredmény egy Dávid-csillag. Ennek a körvonala az eredeti három 1 méteres szakasz helyett tizenkét 1/3 méteres szakaszból áll, és három helyett 6 csúcsa van. Vegyük most ezt a tizenkét oldalt és ismételjük meg az átalakítást: emeljünk ismét háromszögeket az oldalak középső harmadára. Csináljuk ezt tovább, a végtelenségig. A körvonal részletekben egyre gazdagabbá válik, s egyre jobban hasonlít majd egy eszményi hópehely körvonalához. Ez a Koch-görbe, Hege von Koch svéd matematikus írta le elsőként 1904-ben.1
Ezek a századforduló környékén leírt korai fraktálalakzatok, amiket vállalkozó szellemű matematikusok a technikai hiányosságból adódó nehézségek ellenére megtaláltak, a Koch-görbéhez hasonlóan mind végtelen sok rész hozzáadásával, vagy végtelen sok rész elvételével készültek.
Szintén a 20. század elején felfedezett fraktál alakzat volt a Sierpinski-szőnyeg, ami megtalálójáról Wacław Sierpiński lengyel matematikusról kapta a nevét:

Az Sierpinski-szőnyeg úgy szerkeszthető, hogy egy négyzet kilenc egyenlő részre osztunk, és a középső kilencedét kivágjuk, azután a maradék nyolc kisebb négyzetet szintén kilenc egyenlő részre osztunk és a közepét megint ugyanígy kivágjuk, és így tovább a végtelenségig. Ezt a módszert ugyanezen a minta alapján elvégezhetjük egy szabályos háromszögön is, amennyiben azt négy egyenlő részre osztjuk, és a középső negyedet vágjuk ki, majd ezt ismételjük a megmaradt kicsi háromszögeken. A szőnyegnek háromdimenzióban a Menger-szivacs a megfelelője: egy testnek látszó rácsozat, amelynek végtelen nagy a felszíne, de nulla a térfogata.
A 20. század eleji matematikusok gyorsan elérkeztek a számítási nehézségek állította korlátig, ahogyan a régi biológus elődök sem tudtak mikroszkópok híján továbblépni egy bizonyos ponton. Egy olyan világot vizsgálva, amely egyre finomabb részleteket rejt, a képzelet nem juthat el akármeddig.
Majd csak a 20. század utolsó harmadában, a számítógépek elterjedésével párhuzamosan kezdett a fraktáltudomány kibontakozni az Egyesült Államokban és Európában. A legkülönbözőbb kutatók köreiben lett ismeretes és használatos, – matematikusok, fizikusok, biológusok, vegyészek, informatikusok, közgazdászok – mindannyian a szabálytalanság különböző fajtái között kerestek kapcsolatokat.
A Káosz
A káosz a meglepetések, a nemlinearitás és a kiszámíthatatlanság tudománya. Arra tanít, hogy számítsunk a váratlanra. Míg a legtöbb hagyományos tudomány kiszámítható jelenségeket vizsgál, mint a gravitáció, az elektromosság vagy a kémiai reakciók, a káosztudomány olyan kiszámíthatatlan dolgokkal foglalkozik, amelyeket gyakorlatilag lehetetlen előre megjósolni vagy irányítani, mint például a turbulencia2, az időjárás, a tőzsde, az agyi állapotunk stb. Ezeket a jelenségeket gyakran fraktál matematika írja le, amely megragadja a természet végtelen összetettségét.
A káosznak a 80-as évek óta elterjedt tudományos fogalma nem egy pillanatnyi helyzetre, elrendezésre, állapotra vonatkozik, hanem az időbeli viselkedésre. Mivel bármilyen mennyiség időfejlődése általános értelemben mozgásnak tekinthető, a káosz ebben a modern szóhasználatban a mozgás, a dinamika jellegére utal.
A kaotikus dinamika számos hétköznapi jelenségben megfigyelhető, gondoljunk például hulló falevelek hintázó esésére. Bármennyi ideig követjük is az ilyen mozgást, nem tudjuk megbecsülni, hogy miként folytatódik. Ez éles ellentétben áll az életünk ritmusát megadó (és az élet kialakulásához igen fontos) szigorú szabályossággal, a periodikus dinamikával, mely a Föld Nap körüli, vagy a Hold Föld körüli mozgására jellemző.
A káosz azon a matematikai tulajdonságon alapszik, hogy egyszerű egyenleteknek is lehet elég bonyolult megoldása. Ezen tulajdonságokat nem sajátíthatja ki egyetlen tudományág sem, a káosz minden természettudomány, sőt minden olyan tudomány sajátja, melyben a matematikai leírás hasznosnak bizonyul (például közgazdaságtan).
A kaotikus dinamikát mutató jelenségek alakulása rendkívül érzékeny a kiinduló helyzetre. Azaz fokozott a kezdőfeltételekre mutatott érzékenységük. A gyakorta emlegetett pillangóhatás ennek a tulajdonságnak egy szemléltetése. Az ismert történet úgy hangzik, hogy egy brazil pillangó megrebegteti a szárnyát, és ennek hatására kialakul egy orkán New Yorkban. Ez a kaotikus viselkedés egy létező, fontos tulajdonságnak sarkított, költői túlzás szintű tálalása. Az ilyen jellegű megfogalmazások nem ritkán misztikus, a tudomány szerepét megkérdőjelező értelmezésre vezetnek. De a mondandóját érdemes megjegyezni: felerősödik a határozatlanság. Hiába igyekezünk két azonos falevelet azonos helyzetből leejteni, mozgásuk rövid idő után különböző lesz. Képtelenség minden pillangó szárnycsapását figyelembe venni például a szélerő kiszámításához, a végtelenül pontos kezdeti helyzet meghatározás irreális absztrakció, és ha a jelen állapot megadásában való apró pontatlanság következményei időben gyorsan növekednek, akkor a mozgás gyakorlatilag megjósolhatatlan. Ezért egyetlen mozgás pontos megfigyelése helyett érdemes mozgássokaságot vizsgálni, gyakori módszer áttérni valószínűségi leírásra.
A kaotikus mozgáshoz határozott geometriai szerkezet tartozik. Ez azért lehetséges, mert a részletes megfigyelés azt mutatja, hogy az előrejelezhetetlenség a mozgásnak csak egyértelműen meghatározott tartományain belül áll fenn. Ezen tartományokon kívül a mozgás periodikus, vagy legalábbis közelítőleg az, tehát olyan, mint amit hagyományosan megszoktunk. A mozgás geometriájának vizuális megjelenítéshez egy koordinátarendszeren (állapottérben) történik. Általában egy érdekesen bonyolult alakzat rajzolódik ki, egy fraktál. A kaotikus mozgás kapcsolata a fraktálokkal azt mutatja, hogy a periodikus mozgástól való eltérés minden léptékben jelen van.
A folyadékok keveredése az egyetlen olyan jelenség, ahol szemmel is láthatóak a kaotikus mozgással kapcsolatos fraktális struktúrák. Ebben az esetben ugyanis az állapottér éppen egybeesik a fizikai térrel. Ha mondjuk, kávéban tejszínt keverünk el, szépen látszik az áramlás szétterjedése. Ez a példa jól szemlélteti a káosznak egy kikerülhetetlen következményét is, az irreverzibilitást. Ugyanis a kávé-tejszín esetében, ha már egyszer elkevertük az egyik irányba, hiába próbálnánk az eredeti mozdulatot pontosan ugyanúgy visszafele végezni, a tejszín nem veszi fel a beöntéskor megfigyelt alakját – ahogy azt örvénymentes esetben tenné3. Ez a hibák felerősödésének egy megnyilvánulása. A kezünk nem irányítható végtelenül pontosan, és így lehetetlen, hogy a megfordított keverés annyira hű mása legyen az eredetinek, hogy az egész fraktál tejszín-alakzatot a kiindulásiba vigye vissza.
Fraktálok a művészetben
Mint láthatjuk a fraktál-geometria vizuális megjelenítése nem a művészek köréből érkezett, hanem a computertechnika adta lehetőségek hívták életre, és bonyolult rendszerek kijelzéseként került felhasználásra. A mögöttük rejlő számításokat eredetileg csak a szakemberek szűkebb köre értette. Viszont amikor ezek a színes ornamentumok bekerültek a köztudatba, hirtelen nagyon népszerűvé váltak. Ahogy kikerültek a tudósok privilégiumából, és a laikusok képernyőin is megjelenhettek, szinte pillanatok alatt hódították meg a vizuális kultúra legkülönbözőbb tartományait. Sokan voltak, akik csak azért vettek számítógépet, hogy a képernyőn megjeleníthessék, és esetleg ki is nyomtathassák az egyes alakzatok kinagyítható lenyűgöző részleteit. A matematikában otthonosabbak pedig néhány új fraktál-képletre is rátalálhattak, és így “saját“ fraktál-geometriai képeket produkálhattak.
Ennél tovább azonban még a komputertechnika virtuózai vagy a vizuális kultúra ezermesterjei sem jutottak, a matematikai háttér túlságosan bonyolultnak bizonyul ahhoz, hogy ezen tovább lépjenek az emberek. Azóta elapadt a fraktálok körüli amatőr lelkesedés, és a fraktálgeometria visszatért a szűkebb szakterületükre, eredményeik pedig beépültek a különböző tudományágakba.
Akadnak azonban jó páran, akik képzőművészként is figyelemreméltóan nyúlnak a fraktálok világához. Drégely Imre munkássága ezt jól példázza.
Drégely Imre
Képei sajátos szisztéma alapján készült fotómozaikok, képek a képekben, többértelmű vizuális élményt kínálva.
A szisztéma kiépülése Polaroid-kollázsokkal kezdődött az Iparművészeti Főiskolán töltött évei alatt, sokat inspirálódott David Hockney Polaroid-kollázsai után és erre építette fel 1992-es diplomamunkáját a Zodiákus sorozatot. Öt csillagképet rakott össze, egyenként 16-16 képkockából, egy fiktív falinaptár lapjaiként jelentek meg, és egy asztrológiai témájú szakdolgozat társult hozzájuk.


Ez a mozaik-szisztéma átterjedt a hagyományos fekete-fehér munkáira is, nagyméretű, néhány képből álló fekete-fehér fotókonstrukciókkal folytatódott a módszer kiforrása. Ilyen technikával készült kompozit csendéletekkel, térkompozíciókkal diplomázott 1994-ben a Mesterképzőn, majd ebből eljutott a több ezer képkockából álló, nagyméretű szekvenciákig.


Ezeket a munkáit 2006-ban mutatta be először önálló kiállításon, Monoszkóp címmel. A Monoszkóp képein a képraszterből ornamensek, sorminták, gépies fraktálok alakultak. A fázisképeken – amik pixelként jelentek meg a nagy egészen – ismerős terek, ipari tárgyak, robotfigurák, bogarak, emberek és hasonlók rendeződnek utópisztikus, gépies rendbe.
A kiállított munkák nagyméretű computerprintek, amelyek digitalizált analóg, illetve digitális fotográfiákból készültek.
A fotókollázsok, fotómátrixok, fraktálok apró képek nagy mennyiségben való egymáshoz rendelésével keletkeznek, sorokba és oszlopokba rendezve. Az így keletkezett ábrák szemünket tesztelik, első látásra monoszkópot, mandalát, ornamentikát, labirintust, szőnyegmintát, kaleidoszkópot vagy dekoratív terülőmintát alkotnak. Közelebbről láthatóvá válnak az egyes, eddig képpontokként ható alkotóelemek.


2006 óta kiállításról kiállításra mutat be lépcsőfokonként alakított kompozit képfajtákat, a szisztémát tovább és tovább gondolva.
A következő lépés a fotószerűbb képhatás felé indult, narratívabb képekkel. Új munkái, a Szenzor vagy az Emlékművek, képbe tömörített történetek.
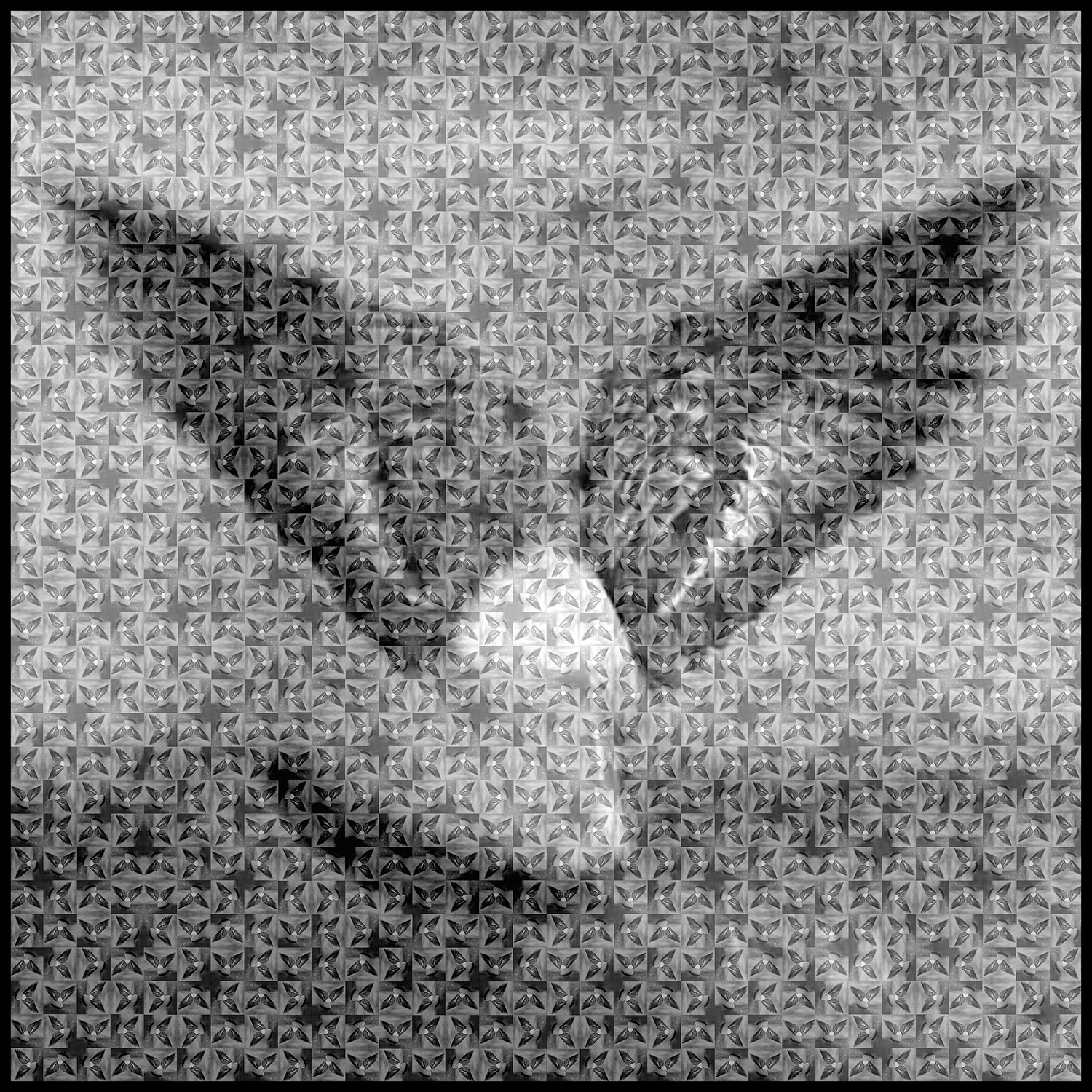
A háttérraszter képei egy konkrét kép textúráját képezik. Szöveggé válnak, arról a konkrét képről szövegelnek. A Szenzor sorozat legtöbb elemének építőkockái a nagy egészből lettek klónozva, tehát minden kicsi képraszter azonos az egésszel.
Ezeknek a képeknek a létrehozása egy igencsak aprólékos és időigényes munka. Drégely manuálisan állítja őket össze, hogy véletlenül se legyen számítógéppel generált kép, saját algoritmus szerint alakítgatja, saját maga kicsinyít, nagyít, állítja be a szemcsézettséget, felbontás, opacitást. Elmondása szerint a munkafolyamat ugyanúgy történik, mint amikor egy hatalmas, készülő festmény előtt szaladgál közelebb-hátrább a festő, csak itt egérrel kell zoomolni.
Gyakran az installálás, a téri dimenzió is része a koncepciónak. Emiatt a képformáláson túl elég nagy szerepe van a léptéknek, és a méretezés beállításának is.
A fényképek nagyításának a történelem során határt szabott a negatív és a pozitív szemcsézettsége: egy bizonyos méret utána a kép egyszerűen szétesett. További nehézséget okozott a tónusos képek átvitele nyomtatásba, ennek megkönnyítésére vezették be a képfelbontásnál a fekete-fehér raszterfilmet.
Drégely ezt a technológiát nemcsak, hogy tovább fejleszti, hanem még feje tetejére is állítja. A rész és az egész viszonyát tekintve, a fraktálokról megszerzett tudásunkat is figyelembe véve, nem egyszerűen „sok kicsiből egy nagyot csinál”, hanem megfordítva, „visszakicsinyít”. Így az aktuális képről nem tudjuk többé, hogy milyen stádiumban van, optimális nagyításban vagy kicsinyítésben, vagy valahol félúton. Bizonytalanná vált, mi a nagyobb vagy teljesebb, a részlet-e vagy az egész.
1 James Gleick: Káosz – Egy új tudomány születése (2004) 74., 78. oldal
2 Az áramlástan jelenségét empirikus módszerekkel vizsgálják (mérésekből származó képletekkel számolnak), ezek alapján keresnek összefüggéseket különböző modellekhez. Tehát bizonyos részei megjósolhatatlanok, azonban nem feltétlen szükséges minden részlet pontos ismerete ahhoz, hogy releváns kövtkeztetéseket tudjanak levonni. A turbulencia az áramlástan egy speciális része.
3 Laminar Flow - YouTube
Ez a videó jól szemlélteti folyadékok lamináris (örvénymentes) áramlását.